Thủ Thuật Hướng dẫn Cho hàm số fx có bảng biến thiên như sau: Số nghiệm thực của phương trình 2 x trụ 5 bảng 0 là Mới Nhất
Hoàng Thị Bích Ngọc đang tìm kiếm từ khóa Cho hàm số fx có bảng biến thiên như sau: Số nghiệm thực của phương trình 2 x trụ 5 bảng 0 là được Cập Nhật vào lúc : 2022-03-08 09:07:08 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi tham khảo tài liệu vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.
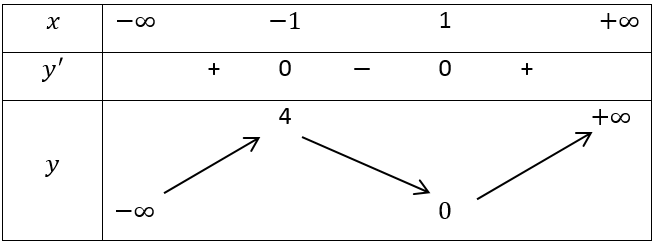
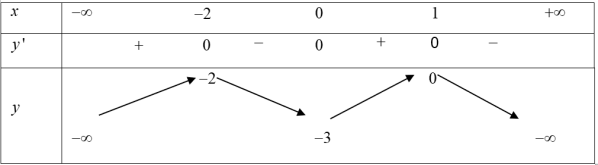
Cho hàm số y=f(x) có bảng biến thiên như sau:
Nội dung chính
- Bài tập cực lớn cực tiểu hàm trị tuyệt đối loại 1 – có đáp ánPhương pháp giải: Loại 2: Cực trị hàm số $y=fleft( left| x right| right).$
Số nghiệm của phương trình f(x) + 7 = 0 là
Giải thích :
Biến đổi f(x) + 7 = 0⇔ f(x) = -7.
Số nghiệm thực của phương trình f(x) + 7 = 0 đó đó là số giao điểm của hai tuyến đường thẳng y = f(x) và y = -7
Dựa vào bảng biến thiên ta có số nghiệm thực của phương trình f(x) + 7 = 0 là một trong.
Ta có: $y=left| fleft( x right) right|Rightarrow y’=fracf’left( x right).fleft( x right) fleft( x right) right$ do đó
Số điểm cực trị của hàm số $y=left| fleft( x right) right|$ là số nghiệm bội lẻ của phương trình $f’left( x right).fleft( x right)=0.$
Như vậy: Nếu gọi m là số điểm cực trị của hàm số $y=fleft( x right)$và n là số giao điểm của đồ thị hàm số $y=fleft( x right)$và trục hoành thì $m+n$ là số điểm cực trị của hàm số $y=left| fleft( x right) right|$ (để ý quan tâm ta cần bỏ đi những nghiệm bội chẵn).
Bài tập cực lớn cực tiểu hàm trị tuyệt đối loại 1 – có đáp án
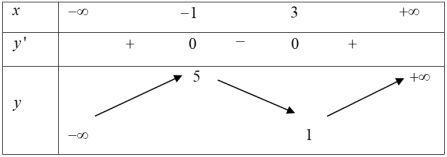
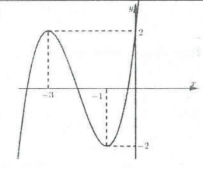
Bài tập 1: [Đề thi THPT QG năm 2017] Cho hàm số $y=fleft( x right)$ có bảng biến thiên như sau.
Đồ thị của hàm số $y=left| fleft( x right) right|$ có bao nhiêu điểm cực trị?
A. 5. B. 3. C. 4. D. 2.
Lời giải rõ ràng
Dựa vào bảng biến thiên ta thấy:
Đồ thị hàm số $y=fleft( x right)$ cắt trục hoành $y=0$ tại 1 điểm nên $m=1.$
Hàm số $y=fleft( x right)$ có 2 điểm cực trị nên $n=2Rightarrow $ Hàm số $y=left| fleft( x right) right|$ có 3 điểm cực trị. Chọn B.
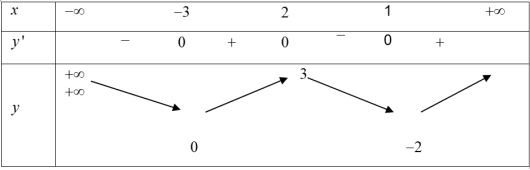
Bài tập 2: Cho hàm số $y=fleft( x right)$ có bảng biến thiên như hình vẽ dưới:
Số điểm cực trị của hàm số $y=left| fleft( x right) right|$là:
A. 3. B. 4. C. 5. D. 6.
Lời giải rõ ràng
Dựa vào bảng biến thiên ta thấy:
Hàm số $y=fleft( x right)$có 3 điểm cực trị suy ra $m=3.$
Phương trình $fleft( x right)=0$ có 3 nghiệm (tuy nhiên $x=-1$ là nghiệm kép) suy ra $n=2.$
Do đó hàm số $y=left| fleft( x right) right|$ có $m+n=5$ điểm cực trị. Chọn C.
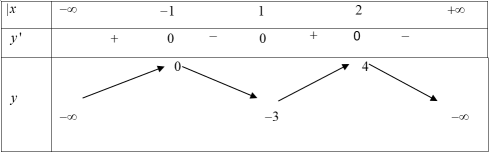
Bài tập 3: Cho hàm số $y=fleft( x right)$ có bảng biến thiên như hình vẽ dưới đây.
Số điểm cực trị của hàm số $y=left| fleft( x right) right|$là:
A. 3. B. 4. C. 5. D. 6.
Lời giải rõ ràng
Dựa vào bảng biến thiên ta thấy:
Hàm số $y=fleft( x right)$có 3 điểm cực trị suy ra $m=3.$
Đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại 3 điểm phân biệt (tuy nhiên $x=-1$ là nghiệm kép) nên $n=2.$
Do đó hàm số $y=left| fleft( x right) right|$ có 5 điểm cực trị. Chọn C.
Bài tập 4: Cho hàm số $y=fleft( x right)$ có bảng biến thiên như hình vẽ dưới đây.
Số điểm cực trị của hàm số $y=left| fleft( x right)+2 right|$là:
A. 4. B. 6. C. 3. D. 5.
Lời giải rõ ràng
Đặt $gleft( x right)=fleft( x right)+2Rightarrow g’left( x right)=f’left( x right)$
Phương trình $g’left( x right)=f’left( x right)=0$ có 3 nghiệm phân biệt nên $m=3.$
Phương trình $gleft( x right)=0Leftrightarrow fleft( x right)=-2$ có 3 nghiệm trong đó có một nghiệm kép $n=2.$
Do đó hàm số $y=left| fleft( x right)+2 right|$có 5 điểm cực trị. Chọn D.
Bài tập 5: Số điểm cực trị của hàm số $y=left| left( x-1 right)^3left( x-3 right)left( x+2 right) right|$ là:
A. 4. B. 5. C. 6. D. 7.
Lời giải rõ ràng
Ta có: $y=fleft( x right)$ thì $y’=fracf’left( x right)fleft( x right)$
Xét $fleft( x right)=left( x-1 right)^3left( x-3 right)left( x+2 right)$
Ta có: $fleft( x right)=0$ có 3 nghiệm bội lẻ $x=1,x=3,x=-2.$
Lại có: $fleft( x right)=left( x-1 right)^3left( x^2-x-6 right)Rightarrow f’left( x right)=3left( x-1 right)^2left( x^2-x-6 right)+left( x-1 right)^3left( 2x-1 right)$
$=left( x-1 right)^2left[ 3x^2-3x-18+left( x-1 right)left( 2x-1 right) right]=left( x-1 right)^2left( 5x^2-6x-17 right)=0Rightarrow f’left( x right)=0$ có 2 nghiệm bội lẻ. Do đó hàm số đã cho có 5 điểm cực trị. Chọn B.
Bài tập 6: Số điểm cực trị của hàm số $y=left| x^4+2x^3-x^2-2x right|$ là:
A. 4. B. 5. C. 6. D. 7.
Lời giải rõ ràng
$fleft( x right)=0Leftrightarrow x^4+2x^3-x^2-2x=0Leftrightarrow x^3left( x+2 right)-xleft( x+2 right)=0Leftrightarrow xleft( x^2-1 right)left( x+2 right)=0$có 4 nghiệm bội lẻ.
Phương trình $f’left( x right)=4x^3+4x^2-2x-2=0Leftrightarrow 2left( 2x^2-1 right)left( x+1 right)=0$ có 3 nghiệm bội lẻ.
Do đó hàm số đã cho có $4+3=7$ điểm cực trị. Chọn D.
Bài tập 7: Số giá trị nguyên của tham số m để hàm số$y=left| x^4-4x^3+4x^2+m right|$ có 7 điểm cực trị là:
A. 0. B. 9. C. 8. D. vô số.
Lời giải rõ ràng
Xét $fleft( x right)=x^4-4x^3+4x^2+m$
Phương trình $f’left( x right)=4x^3-12x^2+8x=0Leftrightarrow left[ beginmatrix x=0 \ x=1 \ x=2 \endmatrix right.$ có 3 nghiệm bội lẻ.
Để hàm số $y=left| x^4-4x^3+4x^2+m right|$ có 7 điểm cực trị thì phương trình
$fleft( x right)=0Leftrightarrow x^4-4x^3+4x^2=-m(*)$ phải có 4 nghiệm phân biệt.
Lập BBT cho hàm số $gleft( x right)=x^4-4x^3+4x$ ta được:
Phương trình (*) có 4 nghiệm phân biệt khi $0<-m<1.$
Vậy không còn mức giá trị nguyên của m nào thỏa mãn yêu cầu bài toán. Chọn A.
Bài tập 8: Số giá trị nguyên của tham số m để hàm số$y=left| x^4-4x^3-8x^2+m right|$ có 7 điểm cực trị là:
A. 129. B. 2. C. 127. D. 3.
Lời giải rõ ràng
Phương trình $f’left( x right)=4x^3-12x^2-16x=0Leftrightarrow left[ beginmatrix x=0text \ x=-1 \ x=4text \endmatrix right.$ có 3 nghiệm bội lẻ.
Để hàm số $y=left| x^4-4x^3-8x^2+m right|$ có 7 điểm cực trị thì phương trình
$fleft( x right)=0Leftrightarrow x^4-4x^3-8x^2=-m(*)$ có 4 nghiệm phân biệt. Lập BBT cho hàm số $gleft( x right)=x^4-4x^3-8x^2$ ta được:
Phương trình (*) có 4 nghiệm phân biệt khi $-3<-m<0.$
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Chọn B.
Bài tập 9: [Đề thi tham khảo Bộ GDĐT năm 2022] Có bao nhiêu giá trị nguyên của tham số m để hàm số$y=left| 3x^4-4x^3-12x^2+m right|$ có 7 điểm cực trị?
A. 3. B. 5. C. 6. D. 4.
Lời giải rõ ràng
Đặt $fleft( x right)=3x^4-4x^3-12x^2+mxrightarrowf’left( x right)=12x^3-12x^2-24x;forall xin mathbbR.$
Phương trình $f’left( x right)=0$ có 3 nghiệm phân biệt.
Để hàm số đã cho có 7 điểm cực trị $Leftrightarrow fleft( x right)=0Leftrightarrow gleft( x right)=3x^4-4x^3-12x^2=m$ có 4 nghiệm phân biệt.
Mà $f’left( x right)=0$ có 3 nghiệm phân biệt $Rightarrow fleft( x right)=-m$ có 4 nghiệm phân biệt.
Dựa vào BBT hàm số $fleft( x right)$, để (*) có 4 nghiệm phân biệt$Leftrightarrow -5<-m<0Leftrightarrow min left( 0;5 right)$.
Kết phù phù hợp với $min mathbbZ$ suy ra có tất cả 4 giá trị nguyên cần tìm. Chọn D.
Bài tập 10: Cho hàm số $fleft( x right)=left| 2x^3-3x^2-12x+m+2 right|$. Số giá trị nguyên âm của tham số m để hàm số đã cho có 5 điểm cực trị là:
A. 26. B. 25. C. 8. D. 9.
Lời giải rõ ràng
Dễ thấy hàm số $gleft( x right)=2x^3-3x^2-12x+m+2$ có $y’=6x^2-6x-12=0Leftrightarrow left[ beginmatrix x=-1 \ x=2text \endmatrix right.$
Suy ra hàm số ![]() có 2 điểm cực trị.
có 2 điểm cực trị.
Để hàm số $fleft( x right)=left| 2x^3-3x^2-12x+m+2 right|$ có 5 điểm cực trị thì phương trình
$2x^3-3x^2-12x+m+2Leftrightarrow hleft( x right)=2x^3-3x^2-12x+2=-m$ có 3 nghiệm phân biệt
Dễ thấy $left{ beginmatrix hleft( -1 right)=9text \ hleft( 2 right)=-18 \endmatrix right.Rightarrow hleft( x right)=-m$ có 3 nghiệm phân biệt khi $-18<-mm>-9$
Vậy có 8 giá trị nguyên cần tìm. Chọn C.
Bài tập 11: Có bao nhiêu giá trị nguyên của tham số m để hàm số $fleft( x right)=left| 2x^4-4left( m+8 right)x^2+m-1 right|$ có 5 điểm cực trị?
A. 9. B. 10. C. 8. D. vô số.
Lời giải rõ ràng
Xét hàm số $fleft( x right)=left| 2x^4-4left( m+8 right)x^2+m-1 right|$
TH1: Hàm số $y=fleft( x right)$ có một điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại nhiều nhất 2 điểm nên hàm số $y=left| fleft( x right) right|$ không thể có 5 điểm cực trị.
TH2: Hàm số $y=fleft( x right)$ có 3 điểm cực trị khi $ab<0Leftrightarrow 2.left[ -4left( m+8 right) right]-8.$
Để hàm số $y=left| fleft( x right) right|$ có 5 điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại 2 điểm phân biệt. Vì hàm số $y=fleft( x right)$ có $a=2>0$ nên có BTT như hình vẽ.
Đồ thị hàm số cắt trục hoành (đường thẳng $y=0$) tại 2 điểm phân biệt khi $0ge m-1Leftrightarrow mle 1.$
(Trong trường dấu bằng xảy ra $m=1Rightarrow $ phương trình có 2 nghiệm đơn và một nghiệm kép $x=0$ nên chỉ có thể có điểm cực trị).
Vậy $-8<mle 1.$ Kết hợp $min mathbbZRightarrow $ có 9 giá trị nguyên của tham số m. Chọn A.
Bài tập 12: Có bao nhiêu giá trị nguyên của tham số $min left[ -10;10 right]$ để hàm số$y=left| x^4-2left( m+4 right)x^2+9 right|$ có 7 điểm cực trị?
A. 9. B. 11. C. 10. D. 4
Lời giải rõ ràng
Xét hàm số $fleft( x right)=2x^4-2left( m+4 right)x^2+4$
TH1: Hàm số $y=fleft( x right)$ có một điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại nhiều nhất 2 điểm nên hàm số $y=left| fleft( x right) right|$ không thể có 7 điểm cực trị.
TH2: Hàm số $y=fleft( x right)$ có 3 điểm cực trị khi $ab<0Leftrightarrow 1.left[ -2left( m+4 right) right]-4.$
Để hàm số $y=left| fleft( x right) right|$ có 7 điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại 4 điểm phân biệt. Ta có: $f’left( x right)=4x^3-4left( m+4 right)x=0Leftrightarrow left[ beginmatrix x=0text \ x^2=m+4=x_0^2 \endmatrix right..$
Hàm số có BTT như hình vẽ:
Đồ thị hàm số cắt trục hoành (đường thẳng $y=0$) tại 4 điểm phân biệt khi
$beginarray fleft( pm x_0 right)=fleft( sqrtm+4 right)<0 \ Leftrightarrow left( m+4 right)^2-2left( m+4 right)^2+99Leftrightarrow left[ beginmatrix m>-1 \ m-1.$ Kết hợp $left{ beginmatrix min mathbbZtext \ min left[ -10;10 right] \endmatrix right.Rightarrow m=left 0;1;…10 right\Rightarrow $ có 11 giá trị của m. Chọn B.
Bài tập 13: Có bao nhiêu giá trị nguyên của tham số $min left[ -20;20 right]$ để hàm số$y=left| x^4-2left( m+1 right)x^2+8 right|$ có 7 điểm cực trị?
A. 9. B. 11. C. 12. D. 7.
Lời giải rõ ràng
Xét hàm số $fleft( x right)=x^4-2left( m+1 right)x^2+8$
TH1: Hàm số $y=fleft( x right)$ có một điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại nhiều nhất 2 điểm nên hàm số $y=left| fleft( x right) right|$ không thể có 7 điểm cực trị.
TH2: Hàm số $y=fleft( x right)$ có 3 điểm cực trị khi $ab<0Leftrightarrow 1.left[ -2left( m+1 right) right]-1.$
Để hàm số $y=left| fleft( x right) right|$ có 7 điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại 4 điểm phân biệt. Ta có: $f’left( x right)=4x^3-4left( m+1 right)x=0Leftrightarrow left[ beginmatrix x=0text \ x^2=m+1=x_0^2 \endmatrix right..$
Hàm số có BTT như hình vẽ:
Đồ thị hàm số cắt trục hoành (đường thẳng $y=0$) tại 4 điểm phân biệt khi
$beginarray fleft( pm x_0 right)=fleft( sqrtm+1 right)<0 \ Leftrightarrow left( m+1 right)^2-2left( m+1 right)^2+88Leftrightarrow left[ beginmatrix m>-1+2sqrt2 \ m-1-2sqrt2.$ Kết hợp $left{ beginmatrix min mathbbZtext \ min left[ -20;20 right] \endmatrix right.Rightarrow m=left 2;3;…10 right\Rightarrow $ có 9 giá trị của m. Chọn A.
Phương pháp giải: Loại 2: Cực trị hàm số $y=fleft( left| x right| right).$
Ta có: $y=fleft( left| x right| right)Rightarrow y’=fracx x right.f’left( left| x right| right)$ từ đó ta có nhận xét sau:
– Hàm số đạt cực trị tại điểm $x=0.$
– Số điểm cực trị dương của hàm số $y=fleft( x right)$là m thì số điểm cực trị của hàm số $y=fleft( left| x right| right)$ là $2m+1$.
Bài tập 1: Cho hàm số $fleft( x right)=6x^5-15x^4-10x^3+30x^2+1,$ số điểm cực trị của hàm số $y=fleft( left| x right| right)$ là:
A. 4. B. 5. C. 6. D. 7.
Lời giải rõ ràng
Ta có: $f’left( x right)=30x^4-60x^3-30x^2+60x=0$
$Leftrightarrow xleft( x^3-2x^2-x-2 right)=xleft( x-1 right)left( x+1 right)left( x-2 right)$
Lại có: $y=fleft( left| x right| right)Rightarrow y’=fracxleft.left| x right|left( left| x right|-1 right)left( left| x right|+1 right)left( left| x right|-2 right)$đổi dấu qua 5 điểm $x=0;x=pm 1;x=pm 2$ nên hàm số $y=fleft( left| x right| right)$có 5 điểm cực trị. Chọn B.
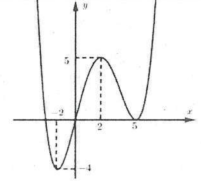
Bài tập 2: Cho hàm số $y=fleft( x right)$ xác định trên $mathbbR$ và có bảng biến thiên như hình vẽ dưới đây.
Số điểm cực trị của hàm số $y=fleft( left| x right| right)$là:
A. 2. B. 3. C. 4. D. 5.
Lời giải rõ ràng
Hàm số $y=fleft( x right)$ có 2 điểm cực trị có hoành độ dương là $left( 2;-1 right)$ và $left( 5;0 right)$
Do đó hàm số $y=fleft( left| x right| right)$ có $2.2+1=5$ điểm cực trị. Chọn D.
Bài tập 3: Cho hàm số $y=fleft( x right)$ có bảng biến thiên như hình vẽ dưới
Số điểm cực trị của hàm số $y=fleft( left| x right|+1 right)$là
A. 4. B. 6. C. 5. D. 3.
Lời giải rõ ràng
Ta có: $y’=left( left| x right|+1 right)’.f’left( left| x right|+1 right)=fracxleft.f’left( left| x right|+1 right)=0Leftrightarrow left[ beginmatrix x=0text \ f’left( left| x right|+1 right)=0 \endmatrix right.(*)$
Dựa vào đồ thị hàm số ta thấy $f’left( x right)=0Leftrightarrow left[ beginmatrix x=-1 \ x=0text \ x=2text \endmatrix right.$
Suy ra $f’left( left| x right|+1 right)=0Leftrightarrow left[ beginmatrix left| x right|+1=-1 \ left| x right|+1=0text \ left| x right|+1=2text \endmatrix right.$hệ có 2 nghiệm.
Do đó (*) có 3 nghiệm phân biệt nên hàm số có 3 điểm cực trị. Chọn D.
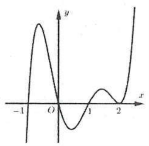
Ví dụ 4: Cho hàm số $y=fleft( x right)$ xác định trên $mathbbR$ và có đồ thị hình vẽ bên.
Có bao nhiêu giá trị nguyên của tham số $m>-20$ để hàm số$y=fleft( left| x right|+m right)$ có 5 điểm cực trị
A. 15.
B. 19.
C. 16.
D. 18.
Lời giải
Ta có: $y’=left( left| x right|+m right)’.f’left( left| x right|+m right)=fracx.f’left( left| x right|+m right)=0Leftrightarrow left[ beginmatrix x=0text \ f’left( left| x right|+m right)=0 \endmatrix right.$
Dựa vào đồ thị hàm số ta thấy $f’left( x right)=0Leftrightarrow left[ beginmatrix x=-3 \ x=-1 \endmatrix right.$
Do đó $f’left( left| x right|+m right)=0Leftrightarrow left[ beginmatrix left| x right|+m=-3 \ left| x right|+m=-1 \endmatrix right.Leftrightarrow left[ beginmatrix left| x right|=-3-m \ left| x right|=-1-m \endmatrix right.$(*)
Hàm số có 5 điểm cực trị khi (*) có 4 nghiệm phân biệt khác 0 $Leftrightarrow left[ beginmatrix -3-m>0 \ -1-m>0 \endmatrix right.Leftrightarrow m-20 \endmatrix right.Rightarrow $ có 18 giá trị nguyên của m. Chọn D.
Ví dụ 5: Cho hàm số $y=fleft( x right)$ xác định trên $mathbbR$ và có đồ thị hình vẽ bên.
Có bao nhiêu giá trị nguyên của tham số $min left[ -10;10 right]$ để hàm số$y=fleft( left| x right|+m right)$ có 7 điểm cực trị
A. 8.
B. 9.
C. 12.
D. 13.
Lời giải
Ta có: $y’=left( left| x right|+m right)’.f’left( left| x right|+m right)=fracx x right.f’left( left| x right|+m right)=0Leftrightarrow left[ beginmatrix x=0text \ f’left( left| x right|+m right)=0 \endmatrix right.$
Dựa vào đồ thị hàm số ta thấy $f’left( x right)=0Leftrightarrow left[ beginmatrix x=-2 \ beginarray x=-2 \ x=5text \ endarray \endmatrix right.$
Do đó $f’left( left| x right|+m right)=0Leftrightarrow left[ beginmatrix left| x right|+m=-2 \ beginarray left| x right|+m=2text \ left| x right|+m=5 \ endarray \endmatrix right.Leftrightarrow left[ beginmatrix left| x right|=-2-m \ beginarray left| x right|=2-mtext \ left| x right|=5-m \ endarray \endmatrix right.(*)$
Hàm số có 7 điểm cực trị khi (*) có 6 nghiệm phân biệt khác 0 $Leftrightarrow left[ beginmatrix -2-m>0 \ beginarray 2-m>0text \ 5-m>0 \ endarray \endmatrix right.Leftrightarrow m<-2.$
Kết hợp $left{ beginmatrix min mathbbZtext \ min left[ -10;10 right] \endmatrix right.Rightarrow $ có 8 giá trị nguyên của m. Chọn A.
Ví dụ 6: Cho hàm số $y=x^3-3left( m-1 right)x^2+6mx+2.$ Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $left[ -100;100 right]$ để hàm số$fleft( left| x right| right)$ có 5 điểm cực trị?
A. 100. B. 99. C. 97. D. 96.
Lời giải
Để hàm số $fleft( left| x right| right)$ có 5 điểm cực trị thì hàm số $y=fleft( x right)$phải có 2 điểm cực trị có hoành độ dương.
Ta có: $f’left( x right)=3x^2-6left( m-1 right)x+6m=0Leftrightarrow x^2-2left( m-1 right)x+2mtext (*)$
Giả thiết bài toán $Leftrightarrow left( * right)$ có 2 nghiệm dương phân biệt $Leftrightarrow left{ beginmatrix Delta ‘=left( m-1 right)^2-2m>0 \ S=2left( m-1 right)>0text \ P=2m>0text \endmatrix right.Leftrightarrow m>2+sqrt3.$
Kết hợp $left{ beginmatrix min mathbbZtext \ min left[ -100;100 right] \endmatrix right.Rightarrow $ có 97 giá trị nguyên của m. Chọn C.
Ví dụ 7: Cho hàm số $y=fleft( x right)=2x^3-3left( m+1 right)x^2+6left( m^2-9 right)x+4.$ Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $left[ -100;100 right]$ để hàm số$fleft( left| x right| right)$ có đúng 3 điểm cực trị?
A. 6. B. 7. C. 8. D. 9.
Lời giải
Để hàm số $fleft( left| x right| right)$ có đúng 3 điểm cực trị thì hàm số $y=fleft( x right)$phải có đúng 1 điểm cực trị có hoành độ dương.
Ta có: $f’left( x right)=6x^2-6left( m+1 right)x+6left( m^2-9 right)=0Leftrightarrow x^2-left( m+1 right)x+m^2-9=0text (*)$
Giả thiết bài toán thỏa mãn khi (*) có 2 nghiệm trái dấu hoặc (*) có một nghiệm bằng 0 và 1 nghiệm dương. TH1: (*) có 2 nghiệm trái dấu $Leftrightarrow m^2-9<0Leftrightarrow -3<m<3.$
TH2: (*) có một nghiệm bằng 0 và 1 nghiệm dương $Leftrightarrow left{ beginmatrix m^2-9=0 \ m+1>0text \endmatrix right.Leftrightarrow m=3.$
Kết hợp hai trường hợp này và điều kiện $left{ beginmatrix min mathbbZtext \ min left[ -100;100 right] \endmatrix right.Rightarrow $ có 6 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. Chọn A.
Ví dụ 8: Cho hàm số $y=fleft( x right)$ xác định và có đạo hàm $f’left( x right)=x^3-left( m+3 right)x^2+2x+4m$ trên$mathbbR$. Số giá trị nguyên của tham số m thuộc đoạn $left[ -100;100 right]$ để hàm số$fleft( left| x right| right)$ có 7 điểm cực trị là:
A. 100. B. 101. C. 198. D. 197.
Lời giải
Để hàm số $fleft( left| x right| right)$ có 7 điểm cực trị thì hàm số $y=fleft( x right)$ có 3 điểm cực trị có hoành độ dương.
$Leftrightarrow f’left( x right)=0$ có 3 nghiệm dương phân biệt.
Ta có: $f’left( x right)=x^3-left( m+3 right)x^2+2x+4m=0Leftrightarrow x^3-3x^2+2x+mleft( 4-x^2 right)=0$
$Leftrightarrow xleft( x-1 right)left( x-2 right)-mleft( x-2 right)left( x+2 right)=0Leftrightarrow left[ beginmatrix x=2text \ gleft( x right)=x^2-left( m+1 right)x-2m=0 \endmatrix right.$
Giả thiết bài toán thỏa mãn $Leftrightarrow gleft( x right)$ có 2 nghiệm dương phân biệt khác 2
$Leftrightarrow left{ beginmatrix Delta >0text \ S=m+1>0text \ beginarray P=2m>0 \ gleft( 2 right)ne 0text \ endarray \endmatrix right.Leftrightarrow left{ beginmatrix m^2+10m+1>0 \ m>0text \ 2ne 0text \endmatrix right.Leftrightarrow m>0.$
Kết hợp $left{ beginmatrix min mathbbZtext \ min left[ -100;100 right] \endmatrix right.Rightarrow $ có 100 giá trị nguyên của m. Chọn A.
Ví dụ 9: Cho hàm số $y=fleft( x right)$ xác định trên$mathbbR$và có đồ thị hình vẽ dưới. Số điểm cực trị của hàm số $fleft( left| x right|+1 right)$ là:
A. 4. B. 6. C. 5. D. 3.
Lời giải
Ta có: $y’=left( left| x right|+1 right)’.f’left( left| x right|+1 right)=fracxleft.f’left( left| x right|+1 right)=0Leftrightarrow left[ beginmatrix x=0text \ f’left( left| x right|+1 right)=0 \endmatrix right.(*)$
Dựa vào đồ thị hàm số ta thấy $f’left( x right)=0Leftrightarrow left[ beginmatrix x=x_1in left( -1;0 right) \ beginarray x=x_2in left( 0;1 right)text \ x=x_3in left( 1;2 right) \ x=2text \ endarray \endmatrix right.$
Suy ra $f’left( left| x right|+1 right)=0Leftrightarrow left[ beginmatrix left| x right|+1=x_1in left( -1;0 right) \ beginarray left| x right|+1=x_2in left( 0;1 right)text \ left| x right|+1=x_3in left( 1;2 right) \ left| x right|+1=2 \ endarray \endmatrix right.Leftrightarrow left[ beginmatrix left| x right|+1=x_3in left( 1;2 right) \ left| x right|+1=2text \endmatrix right.Rightarrow $hệ có 4 nghiệm.
Do đó (*) có 5 nghiệm phân biệt nên hàm số có 5 điểm cực trị. Chọn C.

Clip Cho hàm số fx có bảng biến thiên như sau: Số nghiệm thực của phương trình 2 x trụ 5 bảng 0 là ?
Bạn vừa đọc nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Review Cho hàm số fx có bảng biến thiên như sau: Số nghiệm thực của phương trình 2 x trụ 5 bảng 0 là tiên tiến nhất
Share Link Down Cho hàm số fx có bảng biến thiên như sau: Số nghiệm thực của phương trình 2 x trụ 5 bảng 0 là miễn phí
Quý khách đang tìm một số trong những Chia Sẻ Link Cập nhật Cho hàm số fx có bảng biến thiên như sau: Số nghiệm thực của phương trình 2 x trụ 5 bảng 0 là Free.
Giải đáp thắc mắc về Cho hàm số fx có bảng biến thiên như sau: Số nghiệm thực của phương trình 2 x trụ 5 bảng 0 là
Nếu sau khi đọc nội dung bài viết Cho hàm số fx có bảng biến thiên như sau: Số nghiệm thực của phương trình 2 x trụ 5 bảng 0 là vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Cho #hàm #số #có #bảng #biến #thiên #như #sau #Số #nghiệm #thực #của #phương #trình #trụ #bảng #là – Cho hàm số fx có bảng biến thiên như sau: Số nghiệm thực của phương trình 2 x trụ 5 bảng 0 là – 2022-03-08 09:07:08